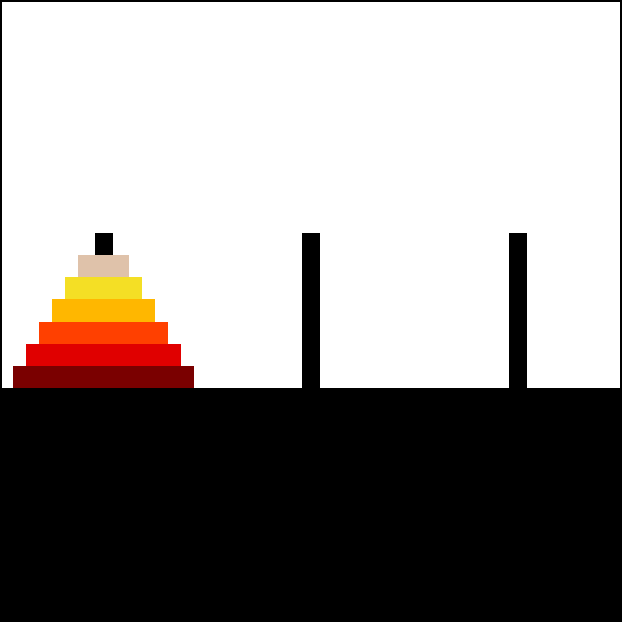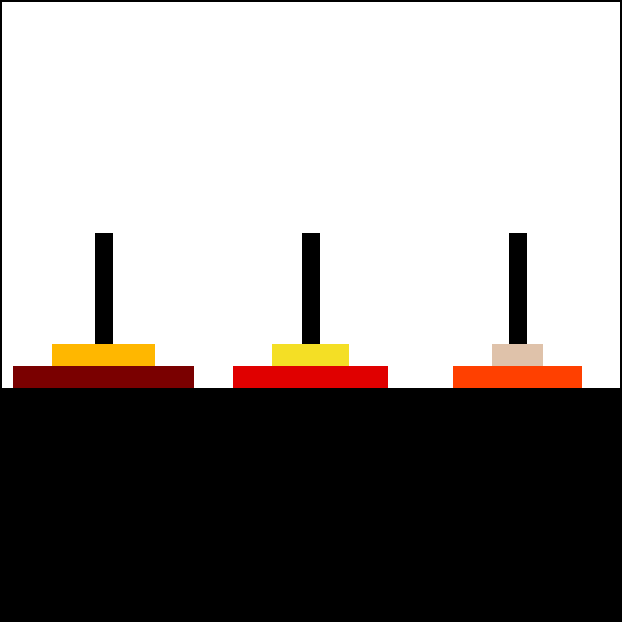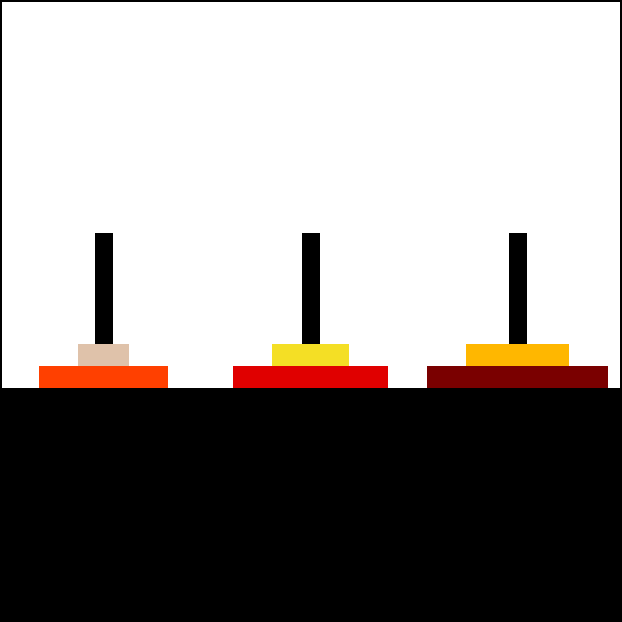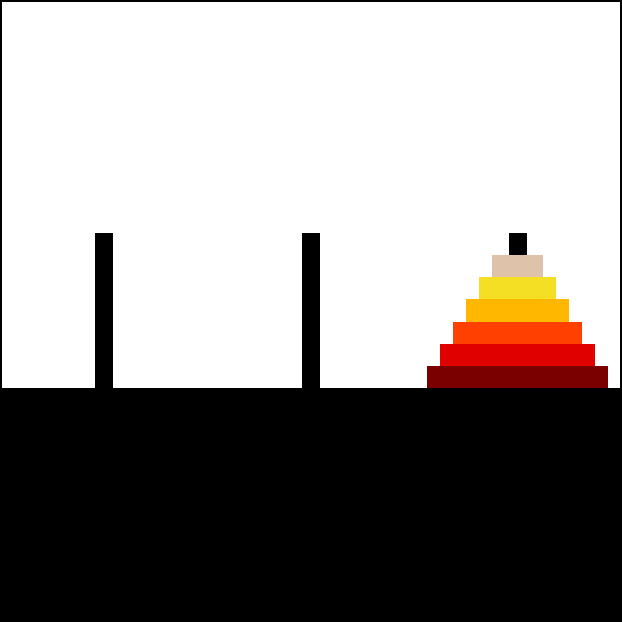theme: Huerta, 5

[fit] Algorithms, not Al Gore's Rhythm

Algorithms

Like any good presentation, let us give the boring definition.

Definition (1/3)

Self-contained step-by-step
set of operations to be
performed.

Definition (2/3)

Algorithms perform calculations,
data processing, and/or
automated reasoning tasks.

Definition (3/3)

An algorithm is an effective
method that can be expressed
within a finite amount of
space and time and in a
well-defined formal language
for calculating a function.

^ WHAAAAAT?

[fit] We use them in life all the time

[fit] Examples

^ Giving specific directions to someone on how to drive from place to place

^ Going to come back to directions later.

http://bit.ly/1tsqopI

^ Followed, created or modified a recipe for cooking

http://bit.ly/1Pp7bZY

^ "Place Tab A into Slot B"

^ Draw two circles

^ Draw the rest of the damn owl

[fit] More formal

^ These are casual examples of algorithms we use or create all the time

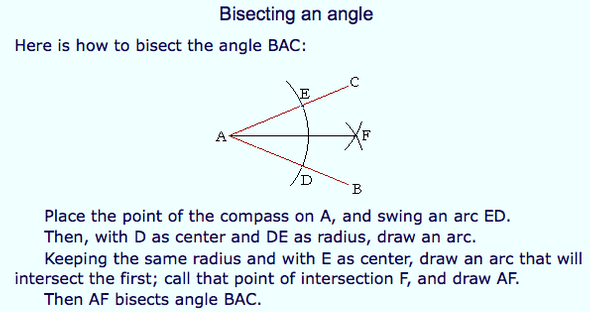
^ Time to bring back that horror of high school math: Geometry

^ Formal construction for bisecting the angle

[fit] Euclid's Algorithm for Computing the Greatest Common Divisor (GCD)

[.column]

English: Given two numbers, A and B,
what is the largest number that
evenly divides **both** numbers

[.column]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 210, B = 45

[.column]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 210, B = 45

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 210, B = 45
A > B (210 > 45)

[.column]

[.code-highlight: 3]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

[.code-highlight: 4]

A = 210, B = 45
A > B (210 > 45)
A = 210 - 45
A = 165

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 165, B = 45

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 165, B = 45
A > B (165 > 45)

[.column]

[.code-highlight: 3]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 165, B = 45
A > B (165 > 45)
A = 165 - 45
A = 120

[.column]

[.code-highlight: 4]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 120, B = 45

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 120, B = 45
A > B (120 > 45)

[.column]

[.code-highlight: 3]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 120, B = 45
A > B (120 > 45)
A = 120 - 45
A = 75

[.column]

[.code-highlight: 4]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 75, B = 45

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 75, B = 45
A > B (75 > 45)

[.column]

[.code-highlight: 3]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 75, B = 45
A > B (75 > 45)
A = 75 - 45
A = 30

[.column]

[.code-highlight: 4]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 45

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 45
else ... since it isn't true that (30 > 45)
B = 45 - 30
B = 15

[.column]

[.code-highlight: 3, 5]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 45
else ... since it isn't true that (30 > 45)
B = 45 - 30
B = 15

[.column]

[.code-highlight: 6]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 15

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 15
A > B (30 > 15)

[.column]

[.code-highlight: 3]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 30, B = 15
A > B (30 > 15)
A = 30 - 15
A = 15

[.column]

[.code-highlight: 4]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 15, B = 15

[.column]

[.code-highlight: 1]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

Euclid's Algorithm for GCD

[.column]

A = 15, B = 15
done with *while*
since A == B
GCD = 15

[.column]

[.code-highlight: 10]

while (A != B) {
 if (A > B)
   A = A - B
 else
   B = B - A
}
return A

[fit] Must be precise and complete

[fit] "Make a PB&J Sandwich."

Example video of a family practicing this.

^ Give a couple of example tries

^ Show that nearly every step we think is precise could be more precise

^ Suggest people try at home

[fit] This is the :key: to mastering programming

^ When starting with algorithms, the more detail we include, even to the point where it may seem silly, the better developers we will be.

1. Read the problem completely twice.
2. Solve the problem manually with several sets of sample data.
3. Optimize the manual steps.
4. Write the manual steps as comments or pseudo-code.
5. Replace the comments or pseudo-code with real code.
6. Optimize the real code.

^ https://simpleprogrammer.com/2011/01/08/solving-problems-breaking-it-down/

Read the problem completely twice.

- Most important!
- Can you explain it (simply) to someone else?

Solve the problem manually

- Programming is automation
- Solve the problem manually
- Maybe even on pen and paper
- Or use physical objects
- Practice!

Optimize the manual solution

- Can you remove any steps?

Write pseudo-code or comments

- Open an editor and write the manual steps in English

Replace comments with real code

- Replace each individual step with code

PEDAC

• Created by Launch School
• Generalized process for creating algorithms:
  • P　 roblem
  • E　 xamples
  • D　 ata (structures)
  • A　 lgorithm
  • C　 ode

Example

[fit] Reverse a string (word)

^ Our goal is to be able to reverse any string (word) ^ How would we break this down into tiny steps

Problem

Given a word, which is just a sequence of letters, make a new word with the same sequence of letters in reverse order.

Examples

^ File.read("/usr/share/dict/words").split("\n").filter { |word| word.reverse == word }.sort_by(&:length)

Data (structures)

• string
• loops

A lgorithm ...

Start by using a specific example...

1. Write “Zebra” down.
2. Create a new empty word.
2. Start at the last letter in the word (the "a" from Zebra)
3. Put the current letter at the end of the new word
4. If there is a previous letter,
   make the previous letter the current letter
   and start back at 3.
5. When there are no more letters in the word, our
   new word is the answer.

Pseudo code

1. NewWord = ""
2. Loop backwards through word to reverse
3.   NewWord += CurrentLetter
4. Return NewWord

Code (Ruby)

word = "Zebra"
new_word = ""
word.chars.reverse_each do |letter|
  new_word += letter
end
new_word # => "arbeZ"

Sorting!

[fit] Simplest Sorting EVAR

Bubble sort

^ https://www.flickr.com/photos/shannonlofthus/4670090955/in/photolist-87Frkz-WHY5B-8mahpK-hN6juM-r7AJpA-ajYWaD-6zd2fV-nhgRbE-86k6Pf-38z42x-indd8g-o92k4j-btkhTp-8as94X-gdM5mg-nuoPxX-8ibJQ1-h2paWu-rqZ7-2wtUmq-7LYqqC-7yGiBn-2VD8P9-bWUbbw-6dXEed-ayCXtz-9VZvt5-ah6cUm-7aNK5e-dM9tRD-bytmvQ-fdgM3t-fMGVce-oDBmtB-fpCiAy-9GxMTc-iALYdC-9gcyYE-e5xtKs-xYMme-5TBqfJ-etJxvL-9TRW6k-4ZPTPC-9JtZ4F-96g9Ms-anRjkS-cqPJ9b-aqFvbJ-85xV3n

For each two adjacent elements

Exchange them if out of order

Repeat until the array is sorted.

Break it down

1. Assume the array is sorted
2. Go through each pair of elements
   - If the first of the pair is larger than the second of the pair
     - Swap the two elements
     - Remember that the array isn't sorted
3. When done with all the elements, if we
   still believe the array is sorted, STOP
4. Otherwise, go back to step 1

^ explain ... in range

^ explain each_cons

array = [7,1,2,9,4,5]
def bubble_sort(array)
  loop do
    # Assume the list is sorted
    sorted = true
    # Go through the indexes of the array in pairs
    (0...array.length).each_cons(2) do |first, second|
      # if the first is larger
      if array[first] > array[second]
        # Swap
        array[first], array[second] = array[second], array[first]
        # Remember array isn't sorted
        sorted = false
      end
    end
    # If array is sorted, stop
    break if sorted
    # end of loop/do go back to the first step
  end
end

• https://github.com/AIRTucha/SortVis

A moment of zen

^ https://www.flickr.com/photos/91604813@N03/8439070389/in/photolist-dRJrBB-s4K1VU-p6DwNY-dRQ271-csLT6L-s5HH9C-53sRLW-p6GeRy-edcCWC-nWCE27-nv6aQE-anoGck-anoFKK-7ius6w-sntwEE-nHEyJ7-anrLr1-ay5Dmf-eijpgL-eimZwd-eidF5v-ekmQMh-anrBX9-dRJrCg-anxCHQ-53oCGD-ay2W6B-54vk5W-anuNNk-anoDX8-anrKnG-dH8fwH-qanAxd-ay5DCW-8VRU3W-poMWLN-ekmnqN-fy8aDK-G78Jjz-anrJWw-anrKLb-anoYUR-5oUwi3-eidEGz-eijpkb-g4cW9M-ein3Yy-eidEQV-b6uVeB-a6v8Lx

^ Moment of zen

[fit] Algorithm Complexity

^ How do we know how "good" our algorithm is?

[fit] Measuring Time and Space

Measure

What are we measuring?

When we speak of algorithm complexity, what are we measuring?

• Operations
• Comparisons
• Increments

^ TODO: Maybe mention Turing Machine here?

Example: Searching

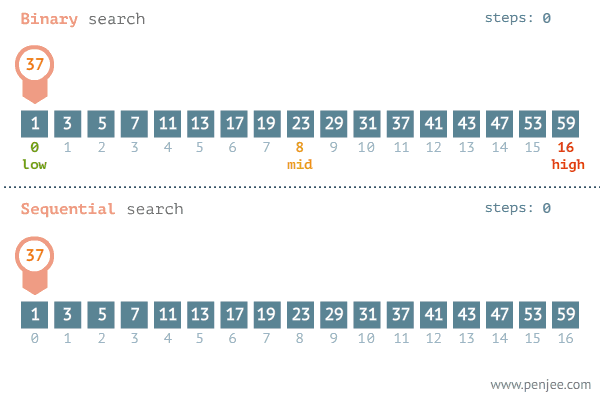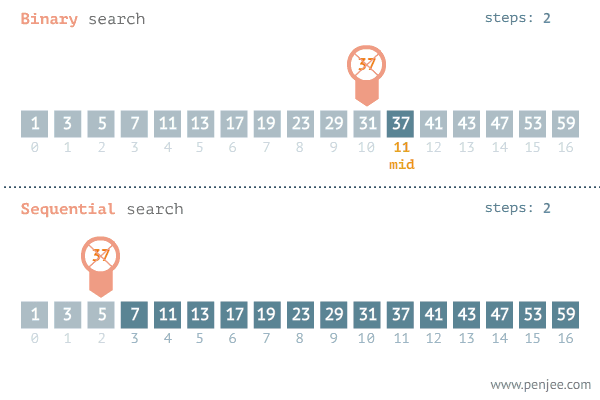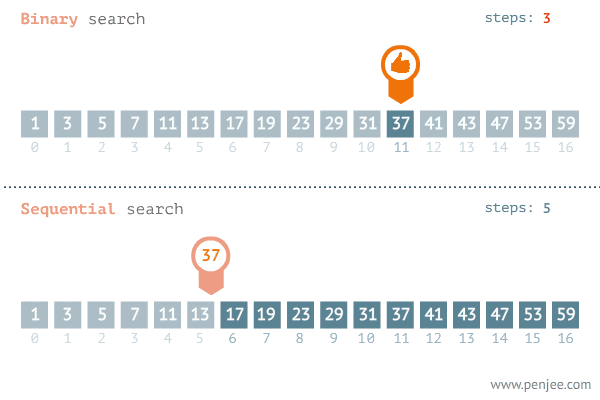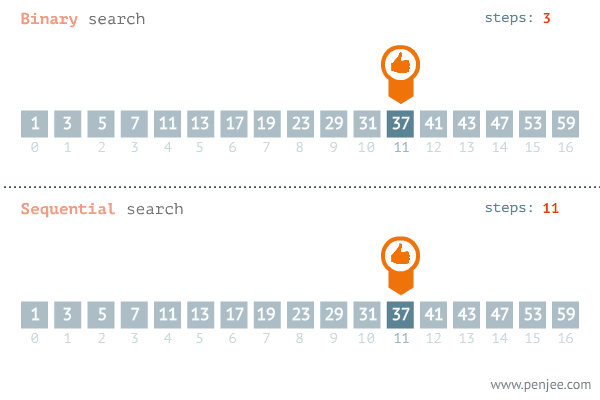
^ Binary search: we half the amount of comparisons we need to do each time we make a decision. This is worst case log(n)

^ The linear search has to compare every element until it finds it. Worst case is O(n)

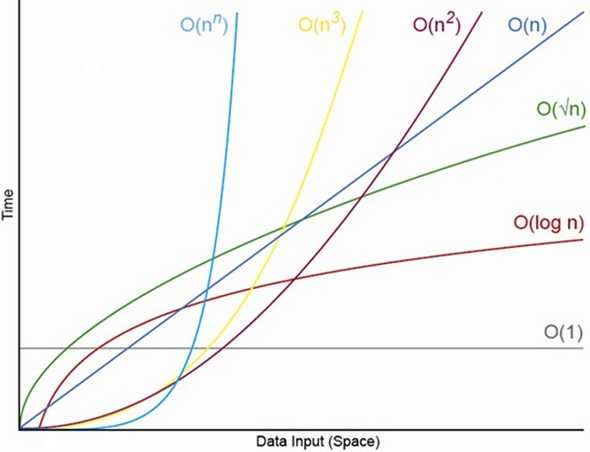
[fit] Big O notation

O(1)

O(log n)

O(n)

O(n log n)

O(n^2)

O(2^n)

• These grow at a different rate based on how n changes

O(1)

Takes a constant amount of time regardless of input size
Example: looking up an index in an array
         looking up a key in a hash/dictionary (most cases)

O(n)

If n doubles, the algorithm takes twice as long
Example: linear search animation

O(n^2)

If n doubles, the algorithm takes FOUR times as long
Example: bubble sort!

O(2^n)

If n doubles, the algorithm takes many times as long
e.g., if n grows from 20 to 40, O(2^n) grows by over a MILLION times
Example: Tower of Hanoi

Tower of Hanoi

The Tower of Hanoi is a mathematical game or puzzle.
It consists of three rods and several disks
of different sizes, which can slide onto any rod.
The puzzle starts with the disks in a neat stack
in ascending order of size on one rod, the smallest
at the top, thus making a conical shape.

Tower of Hanoi

The objective of the puzzle is to move the entire
stack to another rod, obeying simple rules

Tower of Hanoi

1. Only one disk can be moved at a time.
2. Each move consists of taking the upper disk
   from one of the stacks and placing it on top
   of another stack i.e. a disk can only be
   moved if it is the uppermost disk on a stack.
3. No disk may be placed on top of a smaller disk.

[fit] Tower of Hanoi

$$ 2^n $$

[fit] To understand recursion you

[fit] must first understand recursion

[fit] Tower of Hanoi Recursively

Move all but the bottom disk to the
"spare" peg (using this exact algorithm)
Move the bottom disk to the "destination"
peg (this is a simple move)
Move all the disks from the "spare" peg to
the "destination" peg (using this exact
algorithm)

[fit] Tower of Hanoi

Tower of Hanoi

If we could move a disk per second how long would this take?

[fit] Complexity

Salesperson

^ Imagine you are a traveling salesperson.

^ What is the best route for the salesperson to visit each city only once, returning to the starting city at the end?

[fit] Could you find it by hand?

[fit] Probably, for a small number of cities!

1 Billion Computations per second

1 Billion Computations per second

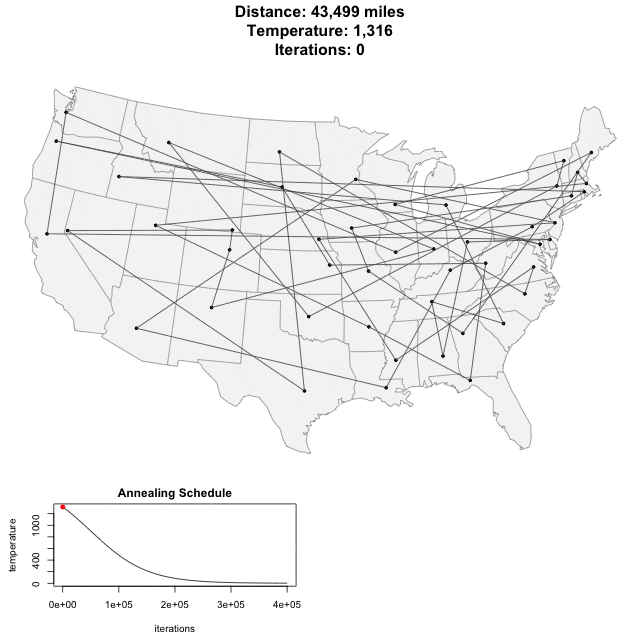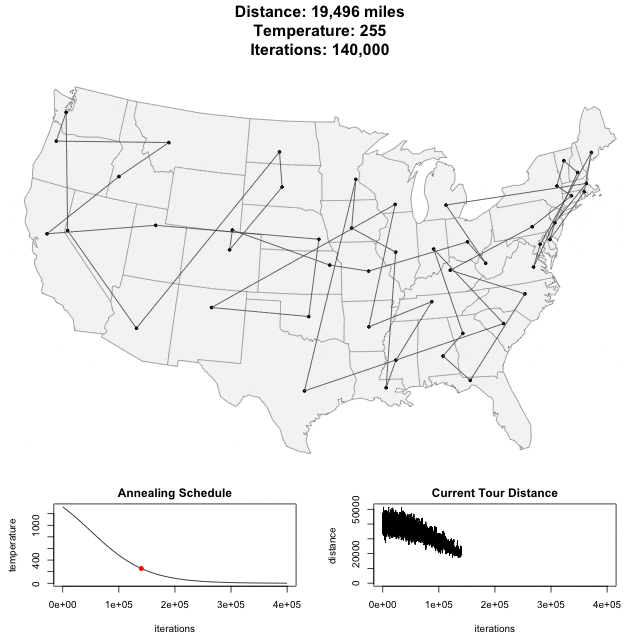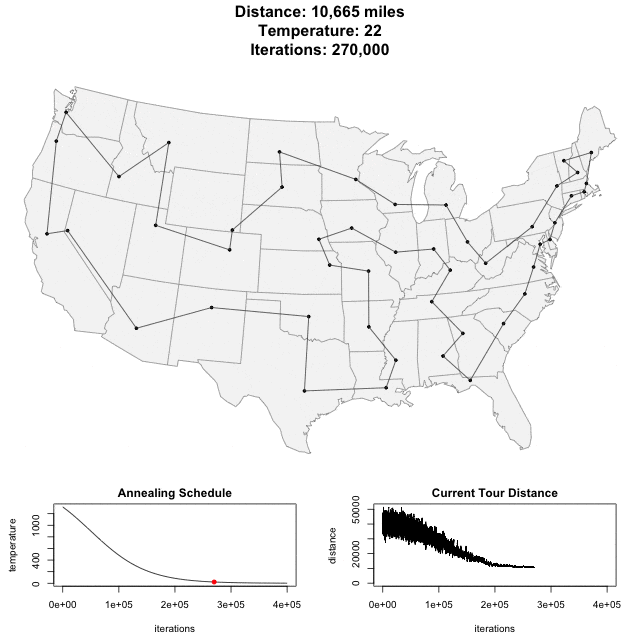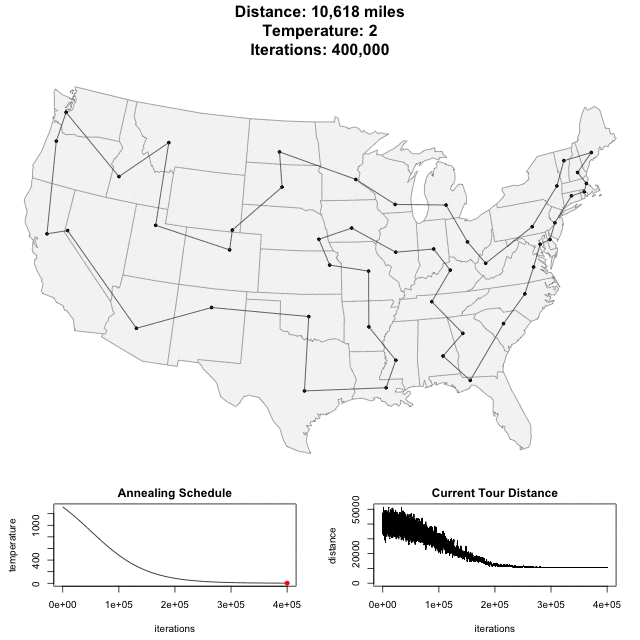
^ Upwards of 400,000 iterations for about 50 cities

The TSP has several applications

planning
logistics
manufacturing of microchips
DNA sequencing

[fit] For More info

[fit] http://bit.ly/XUXLXWX

[fit] Wrap It Up

^ Let's wrap this up

[fit] Algorithms Matter

[fit] Understanding Complexity Matters

Understanding How to Break Problems Down Effectively REALLY Matters

Being a Developer

1. Understanding the problem
2. Break it down into small steps
3. Break it into even smaller steps
4. Translate this to code
5. Appreciate the complexity

How to practice?

exercism.io
codewars.com
CoderNight meetup
(http://meetup.com/CoderNight)

[fit] Thank You

[fit] Questions?